Federgraph 2023
Zuletzt aktualisiert am 20.05.2023.
Achtung, neues Projekt: Federgraph, in seiner Eigenschaft als Skulptur, soll gebaut werden! Dabei kann der Maßstab verändert werden, sowie für die einzelnen Schichten:
- die Basishöhe (CapValue),
- die Dicke (SliceHeight),
- der Mesh-Typ (RingGroup, Slice, Roof, Hand),
- und hoffentlich auch die Farbe.
Als Farbe kann hier auch die spezielle Ausstrahlung eines bestimmten Materials gelten. Dreimal dürfen Sie raten, warum die Farbe wichtig ist, bzw. warum es sinnvoll sein könnte, die Skulptur aus mehreren Teilen zusammenzusetzen.
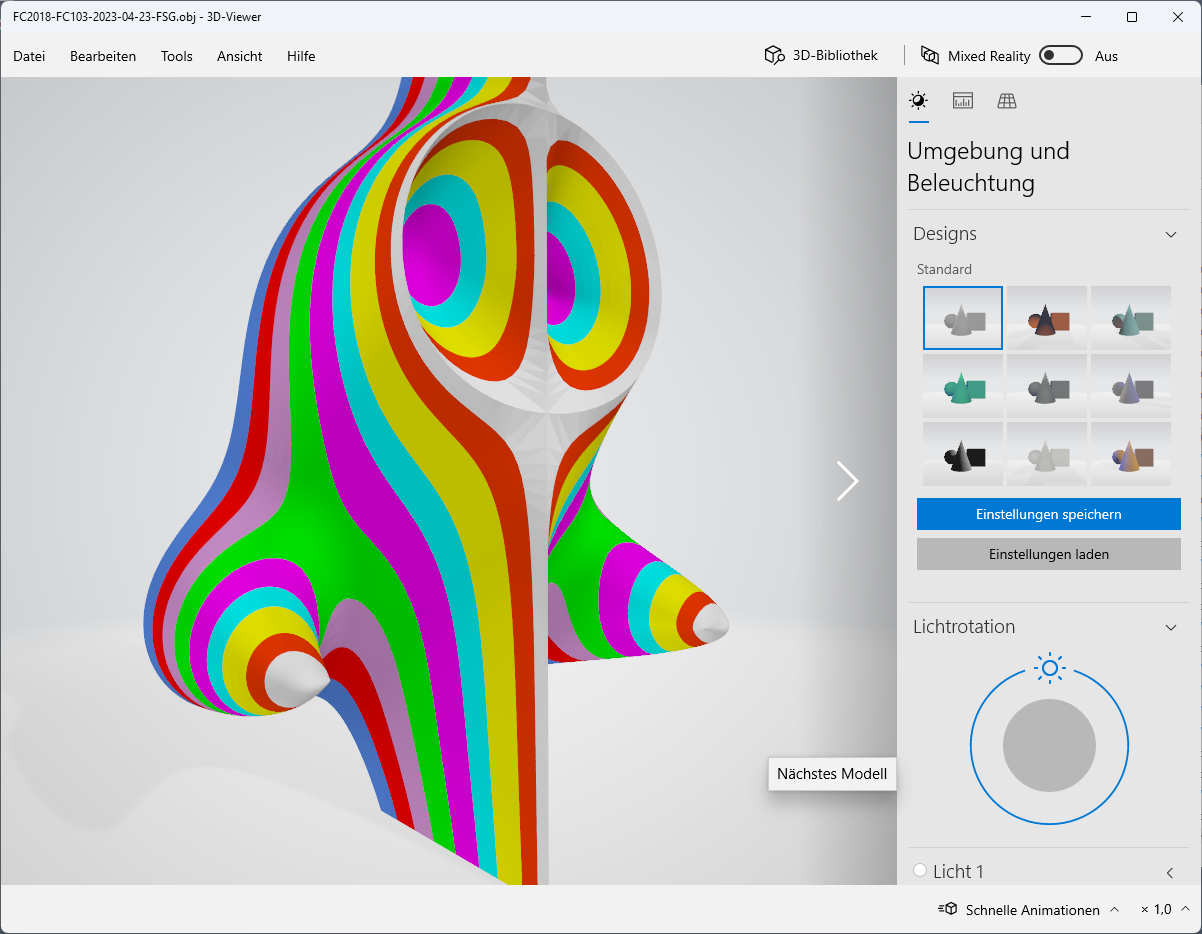
Die Applikation FC103 (Bild weiter unten im Text) kann Mesh-Daten im .obj Format exportieren, welche mit Doppelklick in die Microsoft App 3D-Viewer geladen werden können, siehe Bild oben und unten.
Die Skulptur könnte auch aus nur einem einzigen Mesh bestehen, dann wird es aber schwieriger mit den Farben. Wenn aus Porzellan gefertigt, dann müsste die Figur von Hand bemalt werden.
Vorteil: Bei Verwendung von mehreren Schichten kann jede einzelne Schicht optimiert werden, zum Beispiel durch die Verwendung des jeweils am besten geeigneten Mesh-Builder-Typs.
Die Kombination von unterschiedlichen Mesh-Builder Typen ist die Grundlage für das neue Projekt. Der bisher verwendete Typ ist allgemein verwendbar und wurde zuletzt verbessert, andere wurden für die spezielle Situation entwickelt.
Eine neue Linie in der Entwicklung betrifft den Mesh-Builder. Unabhängig vom verwendeten Mesh-Builder Typ ist aber die Formel für die Berechnung der z-Koordinaten der Vertices immer die gleiche.
Sie können die Theorie überspringen und direkt zur Download-Seite wechseln. Dort wird es schneller konkret. Die folgenden Abschnitte enthalten Hintergrund-Informationen zum Thema.
Bild mit nur einer Feder
Für eine einzelne Feder mit linearer Kennlinie ergibt sich die folgende Situation:

Das ist sicherlich keine Überraschung.
- Die Länge der Feder ist normalerweise immer positiv.
- Negative Werte für x können als Richtungsumkehr interpretiert werden.
- Die Bildung des Betrages der Kraft entspricht einer Spiegelung an der x-Achse.
- Beachten Sie, dass die vertikale Achse mit z beschriftet ist.
- Es kann auch über der Ebene (x, y) geplottet werden, anstatt nur über der x-Achse.
- Dann entspricht t1 dem Abstand vom Ursprung, dem Radius.
- Die Rotationsfigur um die z-Achse wäre ein Kegel, bzw. ein eingestülpter Kegel.
- Das Bild wäre dann eine Fläche im Raum, an Stelle einer Linie im 2D-Diagramm.
Bei einer Zusammenschaltung von mehreren Federn würde sich das dreidimensionale Bild aus der Überlagerung von mehreren eingestülpten Kegeln ergeben.
Die Funktion z = f (x, y) ist fast überall stetig und differenzierbar, das ist sehr gut. Es ist die Anwendung der Absolut-Funktion, die harte Kanten oder Spitzen erzeugt, und für Probleme verantwortlich ist. Es kann sinnvoll sein, bestimmte Berechnungen mit der Funktion durchzuführen, bei der die Absolutwert-Bildung noch nicht vorgenommen wurde.
Natürlich gibt es 3D-Bilder basierend auf dem Modell mit nur einer Feder. Wenn zum Beispiel die Befestigungspunkte von mehreren Federn auf die gleichen Koordinaten eingestellt werden, dann sieht es so aus, als ob nur eine einzelne Ersatz-Feder im Spiel ist, und es erscheint in der Tat ein Kegel, wenn man die Kraft plottet, siehe App.
Modell mit drei Federn
Das der Rechnung zu Grunde liegende Modell hat drei Federn. Jede Feder hat zwei Enden, ein fixes Ende und ein bewegliches Ende. Es handelt sich prinzipiell um ein räumliches Modell.
Die Koordinaten der drehbar gelagerten Endpunkte sind immer dreidimensional. Der Zeichnung unten kann entnommen werden, dass l1 die Länge von Feder 1 im unbelasteten Zustand ist.

Die freien Enden der Federn werden in Punkt P verbunden, welcher in der Ebene z = 0 bewegt wird:
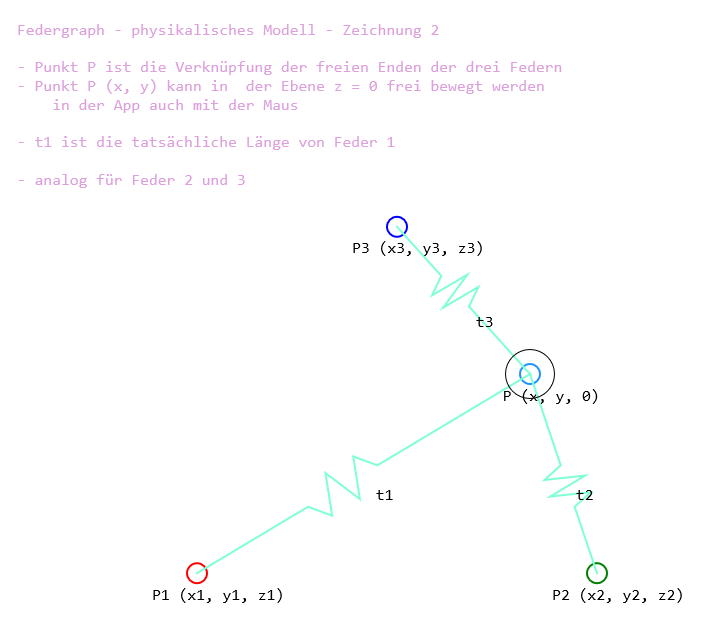
Für jeden Punkt P in der Ebene können nun die Kräfte in den einzelnen Federn ermittelt werden, und anschließend auch die resultierende Kraft, die erforderlich ist, um das System im Punkt P im Gleichgewicht zu halten. Die Zeichnung oben soll zeigen, dass die tatsächliche Länge von Feder 1 mit t1 bezeichnet wird. Das ist wichtig für die Interpretation der Formel.
Formel
Die Federgraph Formel ist immer noch gültig.
Jedoch wurden, für die Skulptur, die konkreten Werte nochmal leicht verändert.
procedure TFederEquationSpecial.Reset;
begin
x1 := -64.95;
x2 := 64.95;
x3 := 0;
y1 := 37.5;
y2 := 37.5;
y3 := -75;
z1 := 0;
z2 := 0;
z3 := 0;
l1 := 90;
l2 := 90;
l3 := 90;
k1 := 1;
k2 := 1;
k3 := 1;
fcap := 500000;
end;
Die Entscheidung bezüglich der konkreten Werte für die Parameter ist also gefallen. Jedoch hat sich gezeigt, dass es noch Bedarf gibt zu erläutern, wie die Formel ursprünglich hergeleitet wurde.
Dazu ist es mit einiger Sicherheit am besten, sich als erstes ansehen, wie die resultierende Kraft, herrührend von den drei Federn, berechnet oder konstruiert werden kann.
Betrag der resultierende Kraft, Variante 1
Es geht relativ einfach, wenn man vorhandene Typen wie zum Beispiel TPoint3D verwendet. Man denke sich TPoint3D als Vektor.
function TFederEquationSpecial.GetForceValue(x, y: single): single;
var
P1, P2, P3, P: TPoint3D; // ein TPoint3D ist ein 3D Vektor.
F1, F2, F3: single;
R1, R2, R3: TPoint3D;
FV1, FV2, FV3, FV: TPoint3D;
begin
P1 := TPoint3D.Create(x1, y1, z1);
P2 := TPoint3D.Create(x2, y2, z2);
P3 := TPoint3D.Create(x3, y3, z3);
P := TPoint3D.Create(x, y, 0);
{ t1, l1, k1: single; // declared at class level }
t1 := (P-P1).Length;
t2 := (P-P2).Length;
t3 := (P-P3).Length;
{ Kraft in Feder, Druckkraft ist negativ }
F1 := k1 * (t1 - l1);
F2 := k2 * (t2 - l2);
F3 := k3 * (t3 - l3);
{ Richtung der Kraft in Feder, Einheitsvektor }
R1 := (P - P1).Normalize;
R2 := (P - P2).Normalize;
R3 := (P - P3).Normalize;
{ Force Vector, negative Kraft bewirkt Richtungsumkehr }
FV1 := F1 * R1;
FV2 := F2 * R2;
FV3 := F3 * R3;
{ man denke an den Kräfteplan }
FV := FV1 + FV2 + FV3;
{ Rückgabewert der Funktion ist der Betrag der Kraft, immer positiv }
result := FV.Length;
end;
- Kraft-Wert F1 ist ein Skalar, hier vom Typ single, kann negativ sein.
- Die Richtung der Kraft in der Feder ist gegeben durch den Einheitsvektor in Richtung der Kraft.
- Die Kraft selbst ist ein Vektor mit Länge und Richtung.
- Die resultierende Kraft ergibt sich durch Addition der Vektoren.
- Der Vektor der resultierenden Kraft schließt den Kräfteplan, hat Betrag und Richtung.
- Die Funktion gibt den Betrag der resultierenden Kraft zurück, die Länge des Vektors, immer positiv.
Natürlich ist es interessant die Stellen zu kennen, wo die resultierende Kraft Null wird. Hier wird aber nur der skalare Wert berechnet, an der Stelle P, um später als z-Koordinate im Mesh verwendet zu werden, wenn der Betrag der resultierenden Kraft, geplottet über der Ebene, im Bild dargestellt werden soll.
Betrag der resultierende Kraft, Variante 2
Die klassische Variante, ohne Vektoren, folgt.
procedure TFederEquationSpecial.InitT(x, y: single);
begin
a1 := sqr(x-x1) + sqr(y-y1);
a2 := sqr(x-x2) + sqr(y-y2);
a3 := sqr(x-x3) + sqr(y-y3);
t1 := sqrt(a1 + sqr(z1));
t2 := sqrt(a2 + sqr(z2));
t3 := sqrt(a3 + sqr(z3));
end;
function TFederEquationSpecial.ResultierendeKraft(x, y: single): single;
var
F1, F2, F3: single;
bf: single;
begin
InitT(x, y);
F1 := k1 * (t1 - l1); // Kraft in Feder 1, Druckkraft ist negativ
F2 := k2 * (t2 - l2);
F3 := k3 * (t3 - l3);
u1 := F1 * (x-x1) / t1; // F1 * x-Komponente von Richtung
u2 := F2 * (x-x2) / t2;
u3 := F3 * (x-x3) / t3;
v1 := F1 * (y-y1) / t1;
v2 := F2 * (y-y2) / t2;
v3 := F3 * (y-y3) / t3;
w1 := F1 * (z-z1) / t1;
w2 := F2 * (z-z2) / t2;
w3 := F3 * (z-z3) / t3;
u := u1 + u2 + u3;
v := v1 + v2 + v3;
w := w1 + w2 + w3;
bf := sqrt(sqr(u) + sqr(v) + sqr(w)); // Betrag F
result := bf;
end;
Punkt P wird zwangsgeführt in der Ebene.
- Die z-Koordinate von P ist immer Null.
- Die vertikale Komponente der resultierenden Kraft wird von der Führung aufgenommen.
Wir interessieren uns daher hauptsächlich für die horizontalen Komponenten, diese werden in den Gleichgewichtslagen zu Null. Da hier im speziellen Fall auch alle Befestigungspunkte in Ebene z = 0 liegen, kann die Berechnung noch vereinfacht werden.
function TFederEquationSpecial.ResultierendeKraftH(x, y: single): single;
var
F1, F2, F3: single;
bf: single;
begin
{ Spezialfall, alle Befestigungspunke liegen in Ebene z = 0, w entfällt }
InitT(x, y);
F1 := k1 * (t1 - l1); // Kraft in Feder 1, Druckkraft ist negativ
F2 := k2 * (t2 - l2);
F3 := k3 * (t3 - l3);
u1 := F1 * (x-x1) / t1; // F1 * Richtungs-Cosinus
u2 := F2 * (x-x2) / t2;
u3 := F3 * (x-x3) / t3;
v1 := F1 * (y-y1) / t1; // F1 * Richtungs-Sinus
v2 := F2 * (y-y2) / t2;
v3 := F3 * (y-y3) / t3;
u := u1 + u2 + u3;
v := v1 + v2 + v3;
bf := sqrt(sqr(u) + sqr(v)); // Betrag der horizontalen Komponente von F
result := bf;
end;
Der zurückgegebene Wert bf in der Funktion oben ist der Betrag der horizontalen Komponente der resultierenden Kraft.
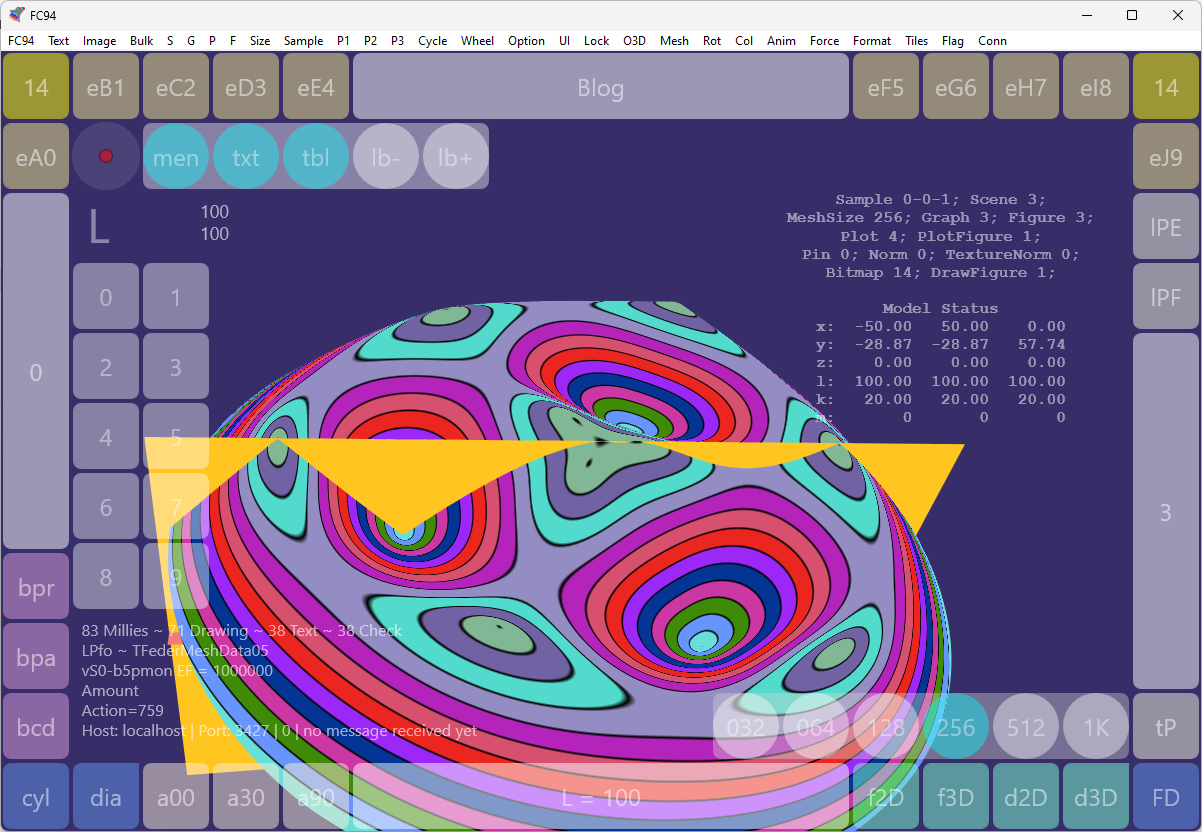
Im nachfolgenden Bild sind die Kräfte eingetragen:

- die einzelnen Kräfte wurden grün gezeichnet
- die resultierende Kraft wurde rot gezeichnet
- das blaue Dreieck verbindet die Befestigungspunkte P1, P2, P3
- die Federn sind ebenfalls blau gezeichnet
- der Screenshot erscheint hier seitenverkehrt, siehe Vorzeichen der x-Koordinate von P1 im Status-Text
- die grauen Kreise haben einen Radius entsprechend l1, l2, l3
- der gelbe Kreis wird um den Koordinatenursprung gezeichnet
- der Radius des gelben Kreises entspricht der Länge von Ortsvektor P
- Der Kräfteplan beginnt im Punkt P
- Punkt P kann in Applikation FC94 mit der Maus gezogen werden
- die Zeichnung aktualisiert sich dann automatisch
Es kann verschiedene Gründe geben, warum das Koordinaten-System in der Praxis abweichend definiert wird. FC103 kann die berechneten Koordinaten auf verschiedene Weise ausgeben, optimiert für Blender oder 3D Viewer, oder nativ. Eine Anpassung an den Bedarf der importierenden Anwendung sollte kein Problem sein.
Und jetzt nochmal zurück zur Formel
Die Seite mit der Federgraph Formel sollte jetzt etwas einfacher zu interpretieren sein, insbesondere wenn man zunächst den Unterschied zur Berechnung des Betrages der resultierenden Kraft feststellt.
Hinweis: Man multipliziere mit t1 * t2 * t3 und man lasse auch noch einiges weg, warum auch immer.
Es kann trotzdem noch ein Bild erzeugt werden.
Natürlich kann man den Betrag der resultierenden Kraft auch direkt plotten, mit Plot 4 bei Verwendung der im Store veröffentlichten App. Die entsprechenden Bilder für spezielle Situationen wurden bereits an anderer Stelle diskutiert.
2D Grafik
Relative neu ist, dass Höhenlinien berechnet, interaktiv dargestellt, und auch als svg Grafik exportiert werden können. Beispiel folgt.
Eine Gruppe von Höhenlinien kann im Prinzip für jede beliebige Höhe berechnet werden. Mehrere Gruppen von Höhenlinien können auch gemeinsam, in einer einzelnen dxf-Datei zusammengefasst, exportiert werden.
Im Bild unten ist zu sehen, dass DWG TrueView von Autodesk die dxf-Daten erfolgreich importieren konnte. Jede Höhenlinie bzw. jede Gruppe von Linien auf gleicher Höhe hat seine eigene Ebene und kann damit separat angezeigt und auch separat gedruckt werden, zum Beispiel maßstabsgerecht in eine PDF-Datei. Mit Druck auf transparente Folie erhält man eine Lehre für die Überprüfung der später zu fertigenden Teile.
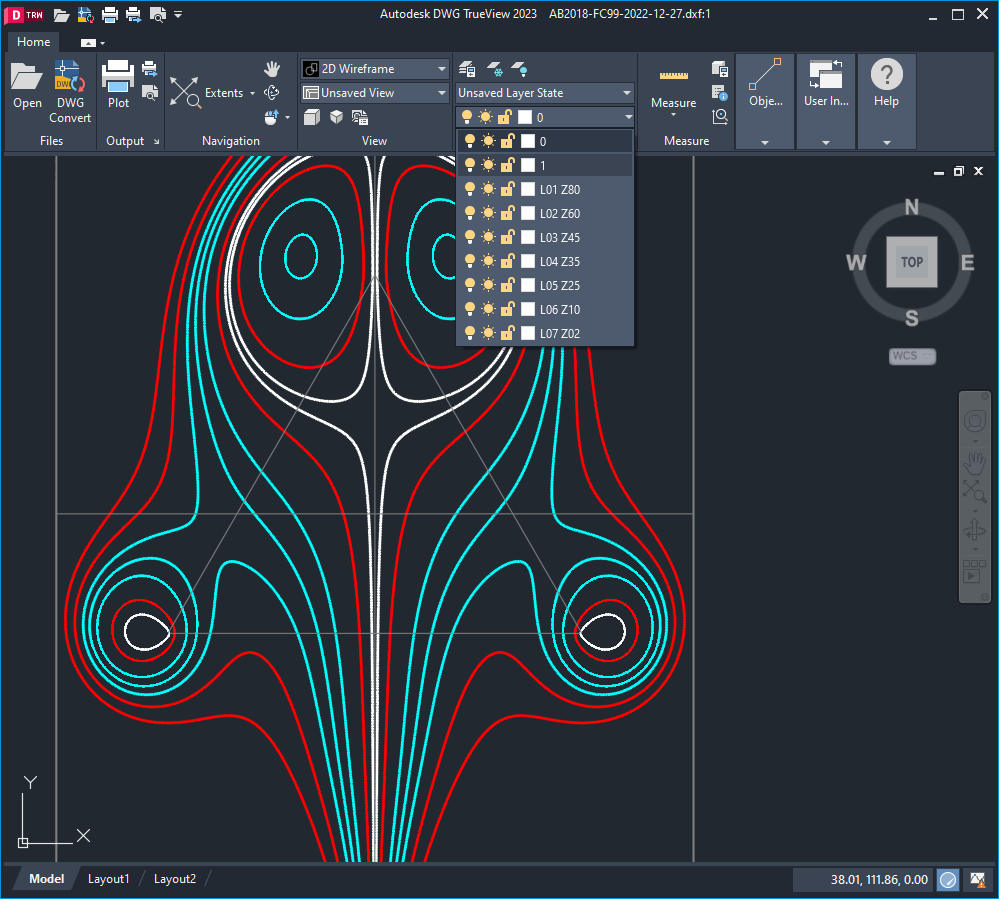
Nur auf Ebene 1 liegt keine Höhenlinie, sondern das Dreieck der Befestigungspunkte und der Rahmen, der die Achsen des Koordinaten-Systems enthält.
- Im Maßstab 1:1 hat die Figur eine Größe, die auf ein Blatt im Format A4 passt.
- Der Rahmen ist 200 mm breit und 280 mm hoch.
- Die y-Achse befindet sich genau in der Mitte des Blattes.
- Der Abstand von P1 und P2 kann gemessen werden zu 2 * 64,95 = 129,9 mm.
- Die x-Achse hat einen y-Offset von 30 mm.
- Die untere Kannte der Skulptur befindet sich bei y = -140 + 30 = -110 mm.
- Die obere Kannte der Skulptur befindet sich bei y = 140 + 30 = 170 mm.
Nachdem dxf-Höhenlinien importiert wurden, ist zu überprüfen, ob der Maßstab stimmt, und dass der y-Offset von 30 mm korrekt eingestellt wurde. Mit anderen Worten, der Ursprung der Zeichnung sollte verschoben werden. Die Lage eines automatisch ermittelten Koordinaten-Ursprungs sollte überprüft und gegebenenfalls korrigiert werden.
Auf ein Blatt A4 gedruckt befindet sich der Ursprung der Figur also nicht in der Mitte des Blattes, sondern 30 mm darunter.
Anhand des mit gedruckten Rahmens kann der Maßstab leicht überprüft werden.
Wenn ein Teil maschinell ausgeschnitten oder ausgefräst werden soll, dann wäre es sinnvoll, die Lage des Koordinaten-Ursprungs geeignet anzugeben, so dass die gefertigten Teile überprüft werden können und auch positioniert und orientiert werden können, und mit benachbarten Teilen verbunden werden können. Genau an dieser Stelle beginnt die gestalterische Freiheit.
3D Mesh-Daten
Ein 3D Teil entsteht dadurch, dass die 3D Fläche an mindestens einer Höhenposition geschnitten wird.
- Null ist oben, garantiert ganz oben wenn die Absolut-Funktion in der Formel überall angewendet wird.
- Die z-Koordinate wächst in positive Richtung nach unter oder hinten.
- Ohne Schnitt würde die Figur in das Unendliche reichen.
- Basishöhe für ein Teil liegt auf Position z = CapValue.
- Zweiter Schnitt liegt auf Position z = CapValue - SliceHeight.
- SliceHeight ist die Dicke eines Teils.
- BaseCap ist die untere Schnittfläche.
- TopCap ist die obere Schnittfläche.
- z = 80 ist unten, z = 0 ist oben.
Bei einzelnen 3D Teilen, deren Mesh-Daten (Stützstellen und Dreiecke, vertices and triangles) als .obj Datei exportiert werden können, wäre zu überlegen, ob die beiden Deckel (die Schnittflächen) oben und unten mit ausgegeben werden sollen, oder ob das importierende Programm den Abschluss selbst machen möchte.

Die durch Schnitte entstehenden Teile werden intern als Slice, Ring, RingGroup oder RingPart bezeichnet. RingPart ist ein zusammengesetztes Objekt, welches die beiden Deckel an Bord hat, siehe Vordergrund im Bild oben.
Ob man durch einen Schnitt eine RingGroup erhält oder nur einen Ring hängt von der Schnittposition ab.
- Wenn eine RingGroup verwendet wird, dann erhält man entweder 1 Teil oder 3 Teile, je nach z-Position.
- Wenn explizit ein Ring verwendet wird, erhält man immer 1 Teil, das erste Teil, eventuell mit zwei Löchern.
Nachdem eine .obj Datei mit mehreren Objekten in Blender importiert wurde, kann man Teile löschen, so dass nur noch das zu fertigende Teil in der Szene verbleibt.
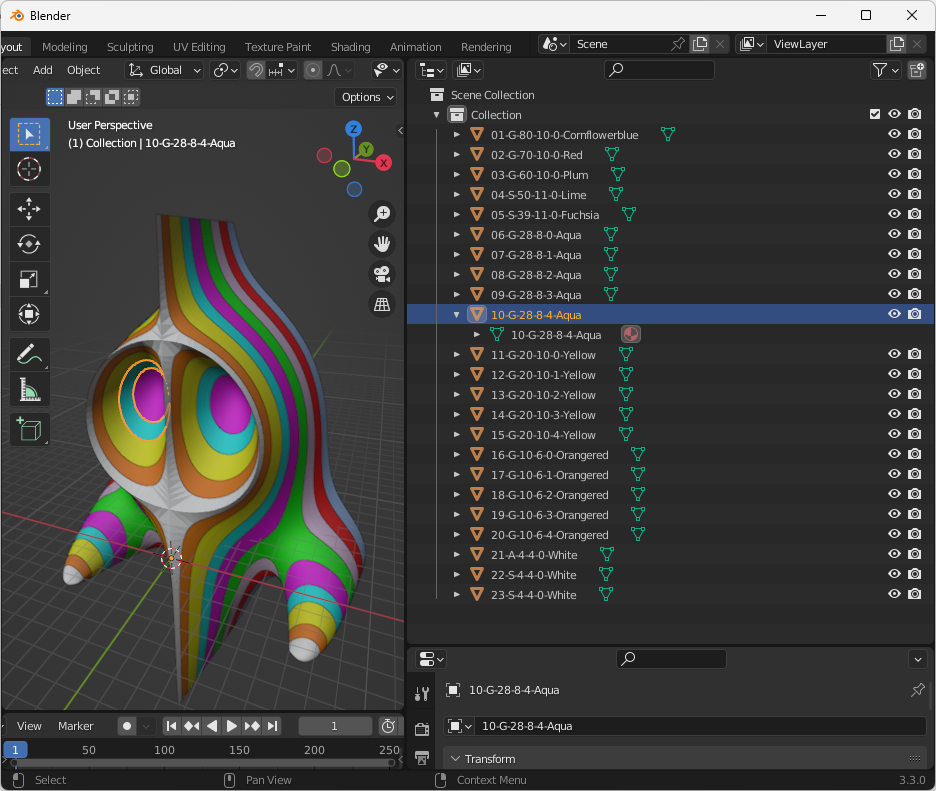
Die Bezeichnung der Teile folgt einem Muster.
ID-MeshType-CapValue-SliceHeight-Mode-Color
Der Mesh-Typ wird mit einem einzelnen Buchstaben wie folgt kodiert:
function TRingInfo.MeshTypeToChar(mt: TMeshType): string;
begin
case mt of
Shape: result := 'E'; // Extruded Shape
Ring: result := 'R';
RingGroup: result := 'G';
Slice: result := 'S';
SliceUpper: result := 'U'; // nicht verwendet
SliceLower: result := 'L'; // nicht verwendet
SliceTop: result := 'T';
Roof: result := 'A';
SlicePart: result := 'X';
RingPart: result := 'Y';
else result := '-';
end;
end;
Wenn das gleiche Bild mehrfach erscheint, dann ist das kein Problem, es wird nur einmal vom Server geladen.
Hier also das gleiche Bild nochmal, um es im Blick zu behalten.

01-G-80-10-0-Cornflowerblue
04-S-50-11-0-Lime
10-G-28-8-4-Aqua
21-A-4-4-0-White
22-S-4-4-0-White
23-S-4-4-0-White
- auf Höhe CapValue = 80 haben wir eine RingGroup mit nur einem Pfad
- auf Höhe CapValue = 50 haben wir ein Slice Objekt mit SliceHeight = 11
- auf Höhe CapValue = 28 haben wir eine RingGroup mit 5 geschlossenen Pfaden
- auf Höhe CapValue = 4 befinden sich drei Objekte, 1 * Roof, 2 * Slice
CapValue sollte immer positiv sein. CapValue = 80 im Maßstab 1:1 passt noch auf ein Blatt A4.
0 < CapValue < 80
SliceHeight muss für MeshType = Slice einen Mindestwert aufweisen. Das Problem entsteht bei der Optimierung. Eine Scheitelpunkt (Vertex) kann nur einmal korrigiert werden, für einen bestimmten z-Wert, und niemals für mehrere z-Werte gleichzeitig. Je dünner die Teile, desto höher muss daher die Auflösung sein, um Fehler zu vermeiden. Die Fehler treten auf, wo die Funktion steil verläuft. Ein 11 mm dickes Teil sollte fast immer funktionieren. Ein nur 10 mm dickes Teil könnte bereits Problemstellen haben.
Es gibt z-Positionen für die zwingend ein Slice-Mesh verwendet werden muss. Dies ist der Fall, wo die 3D Fläche ein Minimum oder Maximum hat wie beim Tiefpunkt der Augen, oder wo sich Sattelpunkte befinden, also zum Beispiel zwischen Hand und Auge.
Ansonsten ist es wahrscheinlich immer besser eine Ring-Gruppe als Mesh-Typ zu verwenden. Ganzzahlwert Mode bezeichnet die Nummer eines einzelnen geschlossenen Pfades in der Höhenliniengruppe, die für die Erzeugung einer RingGroup verwendet wird.
- 0 = Kombination aus 5 und 6 (geschlossener Pfad)
- 1 = Hand Links (geschlossenen Pfad)
- 2 = Hand Rechts (geschlossenen Pfad)
- 3 = Auge Links (geschlossenen Pfad)
- 4 = Auge Rechts (geschlossenen Pfad)
- 5 = Body Links (offener Pfad)
- 6 = Body Rechts (offener Pfad)
Ob Links nicht eigentlich Rechts ist, könnte diskutiert werden, wurde aber bereits festgelegt.
Roof, bzw. das Dach, ist ein Mesh-Typ der speziell für den Abschluss der Pyramide verwendet wird. Es sei erwähnt, dass das Dach zwei Sattelpunkte enthält, das Kreuz des Nordens, und das Kreuz des Südens. Obwohl es anders aussieht, handelt es sich um Sattelpunkte, wo die Tangentenfläche an die Oberfläche horizontal verläuft bzw. wo diese eine vertikale Normale hat. Die Punkte, die so aussehen, als ob sich dort zwei Höhenlinien kreuzen, sind auf alle Fälle interessant, auch bezüglich der Fertigung.

Die Hände sind auch speziell, sie sind normalerweise nach innen geklappt, durch die Absolut-Funktion, können aber auch nach außen geklappt werden. Im Bild oben sind die Hände nach außen geklappt. In diesem Fall kann die Skulptur nicht mehr satt flach auf die Nase gelegt werden, es sei denn, man erzwingt es mit Nachbearbeitung.
Wenn die beiden Hände als separate Slice-Mesh Teile ausgebildet werden, dann lässt sich die Auflösung speziell für diese Teile erhöhen, und sie könnten aus einem abweichenden Material gefertigt werden.
Die Herstellung der oberen Teile, welche die Null-Ebene berühren, gilt als schwieriger im Vergleich zum Teil mit CapValue = 80.
Lizenz erforderlich
Die Befreiung des Projektes steht noch aus.
Alle Teile, wie hier beschrieben, dürfen ausschließlich in limitierter Auflage gefertigt werden, nachdem zuvor eine Lizenz erworben wurde.
Test-Daten für die Entwicklung finden Sie auf der Download-Seite.
Demo
Die ersten gefertigten Teile sind Prototypen bzw. Demo-Objekte. Es sind die Fertigungs-Technologien, die zu demonstrieren sind, anhand des Entwurfs.
Varianten der zu produzierenden Skulptur könnten im nächsten Jahr auf der Messe gezeigt werden, eventuell von verschiedenen Herstellern, in individueller Ausführung.
Selbstverständlich darf man darauf hoffen, das der Wert der geschaffenen Werke steigt, in etwa synchron mit dem Erfolg des Projektes, welches im Bereich STEM verankert ist, und geeignet erscheint, mit dem Bereich Bildung verbunden zu werden.
Vergleichen Sie Federgraph mit anderen dreidimensionalen, mathematisch definierten Figuren, die es schon zur Berühmtheit gebracht haben, und lassen Sie das Auge des Betrachters entscheiden.
Friedenstaube (Version 2.0.20.23)

Federgraph kann verschiedene Formen annehmen, je nachdem welche Formel-Variante ausgewählt wird, zum Beispiel Plot 7 (Taube) an Stelle von Plot 10 (Federgraph).
Skript
Der Aufbau der Skulptur aus einzelnen Teilen kann mit einer Ring-Liste definiert werden. Eine Ring-Liste enthält TRingInfo Elemente. FC103 enthält eine kleine Auswahl fix definierter Beispiele, die mit Button-Click geladen werden können.
Eine Ring-Liste kann auch als Text-Datei bereitgestellt oder vom Memo gelesen werden. Die Text-Form einer Ring-Liste wird dann zunächst in die interne Variante einer Ring-Liste umgewandelt (geparst), und anschließend normal geladen wie die Beispiele.
Eine aktuell im Programm geladene Szene kann als Ring-Listen-Text im Memo auszugeben werden, so dass man ein Beispiel erhält, wie eine Ring-Liste aussehen sollte.

Der Text im Memo könnte herauskopiert, verändert und als .text Datei über das Drop-Target wieder gelesen werden.
type
TExportCoords = (
Native,
App_Blender,
App_3D_Viewer,
App_3D_Printer
);
TMeshType = (
Unknown,
Shape,
Ring,
RingGroup,
Slice,
SliceUpper,
SliceLower,
SliceTop,
Roof,
SlicePart,
RingPart
);
TMaterialType = (
ColorMat,
SimpleMat,
LightMat,
FederMat,
RingMat,
BodyMat,
EyeMat,
HandMat
);
TRingInfo = record
Color: TAlphaColor;
CapValue: single;
SliceHeight: single;
WantPolyTrim: Boolean;
WantMoreDetail: Boolean;
WantSideCaps: Boolean;
OpenMesh: Boolean;
TextureJack: Boolean;
Mode: Integer;
SubdivisionsH: Integer;
MeshSize: Integer;
MeshType: TMeshType;
MaterialType: TMaterialType;
IsHand: Boolean;
IsLeftHand: Boolean;
IsFlippedHand: Boolean;
SkipHands: Boolean;
// code omitted
end;
Kleinere Anpassungen werden erforderlich sein, zum Beispiel wenn Teile etwas größer gefertigt, und die Höhe später nachbearbeitet werden soll, oder wenn die Genauigkeit noch weiter hochgeschraubt werden soll.
Nach Laden einer veränderten Liste muss in FC103 nur noch der Export-Button gedrückt werden, um eine .obj Datei zu exportieren.

Damit eine importierte .obj Datei farbig angezeigt werden kann, muss eine Text-Datei federgraph-material.mtl im gleichen Ordner liegen. Diese Datei enthält alle standardisierten Web-Farben und wird mitgeliefert.